3 idées quand on sèche sur une question de maths
Que l’on soit collégien, lycéen, étudiant, chercheur, il arrive à tout le monde de rester bloqué sur une question mathématique. Si vous avez tourné le problème dans tous les sens ou bien si vous restez sans inspiration devant votre feuille blanche, voici une check liste qui vous permettra peut-être de débloquer la situation :
- Pensez aux raisonnements mathématiques classiques
- Faîtes des essais !
- Regardez les questions précédentes ou les questions suivantes
1. Vous êtes bloqués ? Avez-vous pensé aux raisonnements mathématiques classiques

Vous séchez sur un problème de maths ? Il existe des types de raisonnements bien connus en mathématiques. Ceux-ci sont très classiques, ils peuvent être utilisés du collège à l’université. Ces raisonnements incontournables sont :
- Le raisonnement par l’absurde
- Le raisonnement par récurrence
- Le raisonnement par contraposée
- Le raisonnement par disjonction de cas.
Pour en savoir plus :
Exemple : Dans le problème ci-dessous, l’expression pour tout n, nous inciterait à utiliser le raisonnement par récurrence.

2. Vous êtes bloqués, avez-vous pensé à faire des essais !
Vous bloquez sur une question ? Avez-vous pensé à faire des essais sur des exemples ?
Ce peut être en faisant un schéma ou une figure pour un problème géométrique qui facilitera la visualisation du problème mais ce peut être aussi faire des essais numériques avec des exemples particuliers. Pensez à l’usage de la calculette ! cela pourra être utile par exemple pour conjecturer une limite, un sens de variation, la convergence d’une suite, etc.
Attention, en aucun cas, une multitude d’exemples ne pourront permettre d’affirmer une proposer de manière certaine, mais cette phase est importante en recherche mathématique, elle permet d’une part de s’approprier le problème et d’autre part à émettre une conjecture dans le cadre d’un problème ouvert en particulier. Cette phase peut également permettre de dégager contre-exemple !

Le volume d’un cube est-il proportionnel à l’aire totale de ses faces ?
Par exemple, pour un cube d’arête 1 cm, son volume est de 1 cm3 et son aire est de 6 cm2. Si son arête est de 2cm, le volume est de 8 cm3 et son aire de 24 cm2.
Nous constatons alors qu’il n’y a pas proportionnalité et nous avons par là même un contre-exemple.
3. Vous êtes bloqués, regardez les questions précédentes ou les questions suivantes
Vous bloquez à un stade du problème ? Il arrive souvent que les questions qui suivent contiennent la réponse à la question sur laquelle on bloque. C’est pour cela que l’on conseille de lire l’énoncé dans sa globalité avant de commencer à résoudre les questions.
De même, les questions qui précèdent peuvent souvent vous aider, vous donner des indices. En effet, l’enchainement des questions n’est pas conçu au hasard surtout s’il s’agit d’un problème. L’enchaînement des questions réside en une trame de déductions logiques conduisant au résultat final : la finalité du problème.
Exemple :
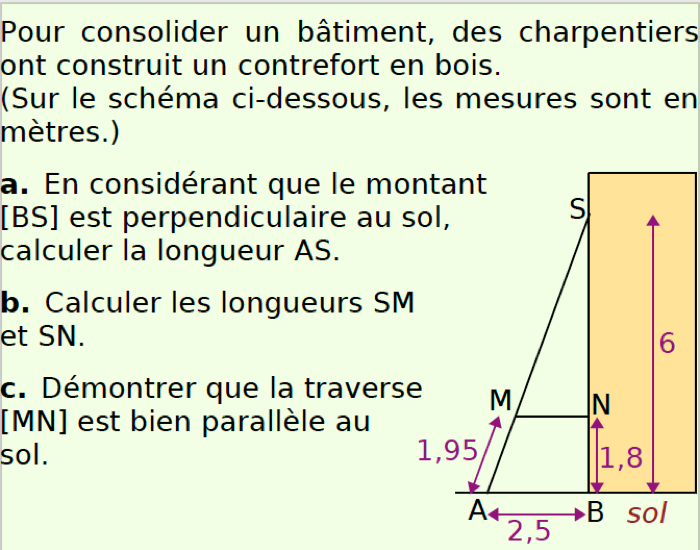
Dans cet exercice, il serait tentant d’utiliser la propriété de Thalès à la question a. pour calculer AS. Et pourtant ce serait une erreur ! En effet, pour utiliser ce théorème il faudrait être sûr que (MN)//(AB), or c’est ce que nous demande la dernière question ! En lisant ce problème entièrement, on constate que sa finalité est de justement de prouver que (MN)// (AB).


Comments are closed.